ビットを複数集めて,2進数とみたてることによって,0以上の整数を表現することが出来る。

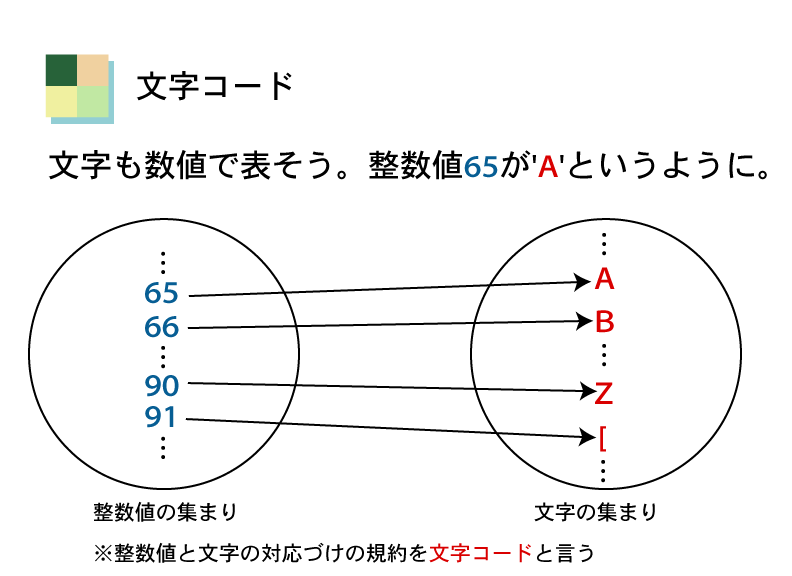
以下の図のように,ある整数値とある文字を対応づけることによって,文字を表現することが出来る。
このように,整数値と対象を対応づけることによって,その対象を表現することをコード化と呼ぶ。
コード化の例としては,県コード,高校コード,商品コードや,書籍コード(ISBNコード)などがある。
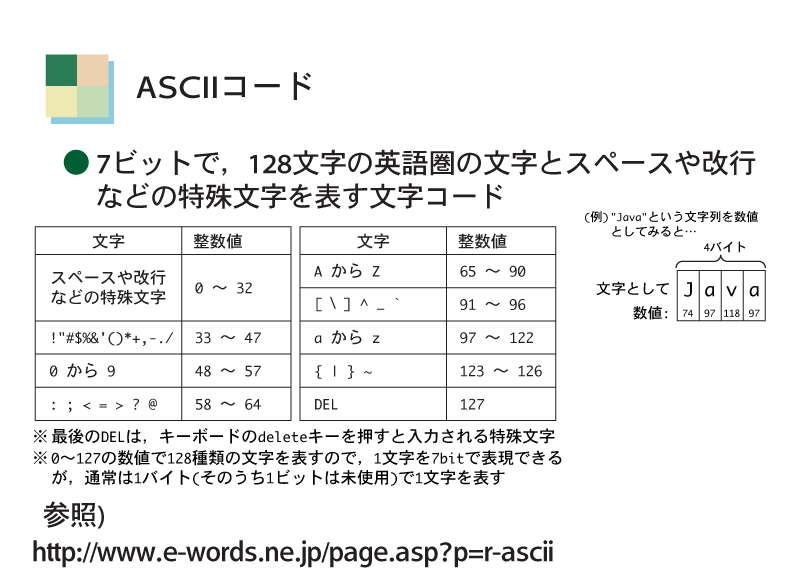
英米圏の文字を7ビットで表現した文字コードをASCIIコードと呼ぶ(下図)。
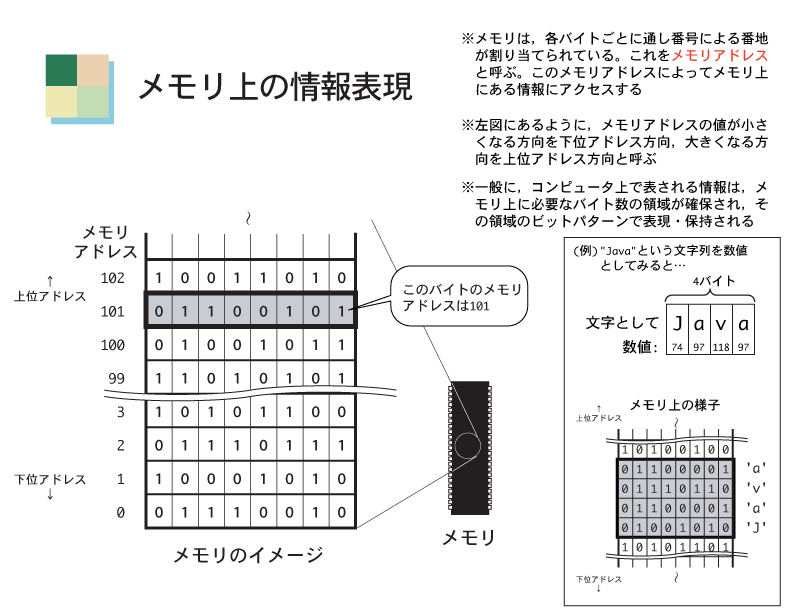
このような情報は,当然,メモリ上のビットで表現されることになる(下図)。
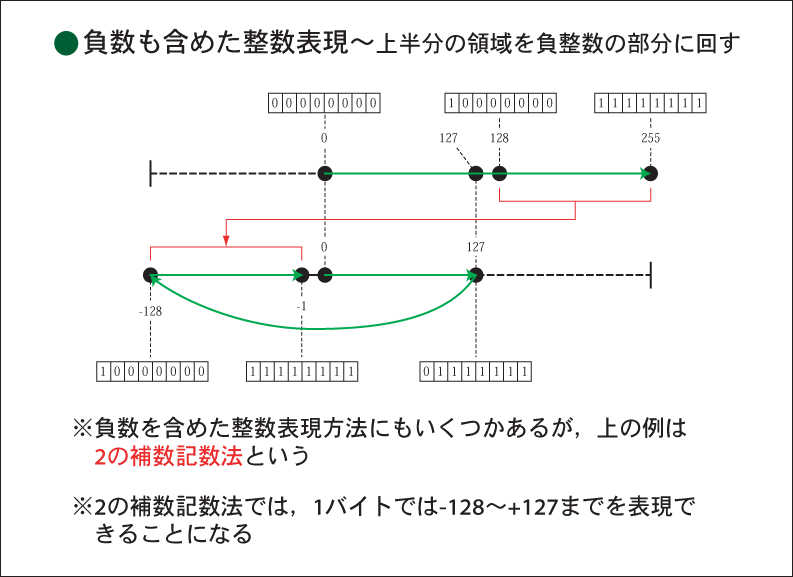
表現方法を学習しよう。方法は簡単で,下図のように0以上の整数を表す場合の,上半分の領域を負の整数の部分
を表現するのに使うのである。この方法を,2の補数基数法と呼ぶ。
つまり,同じビットパターンを「0以上の整数(符号なし整数,unsigned integer)」と扱うか,
「負数を含めた整数(符号付き整数)」と扱うかで,表現している値が異なってくることになる。

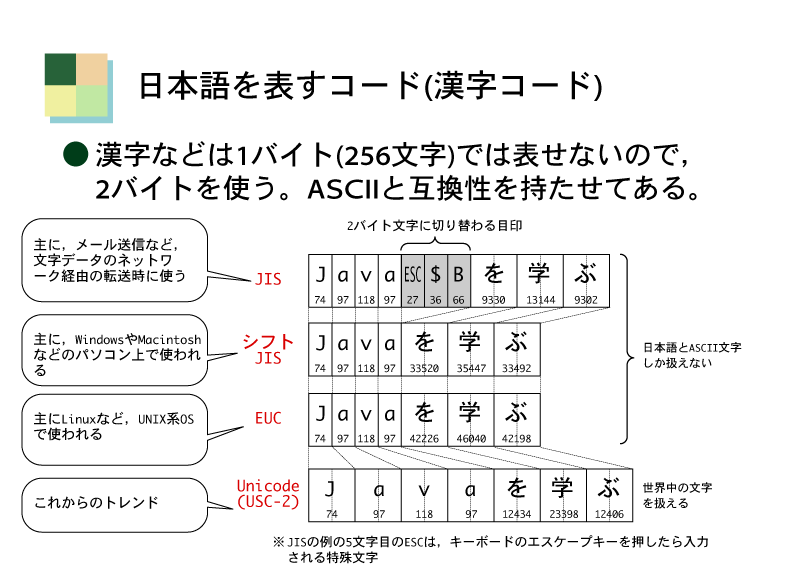
2バイトを使用すると,日本語文字を表現することが出来る(下図)。
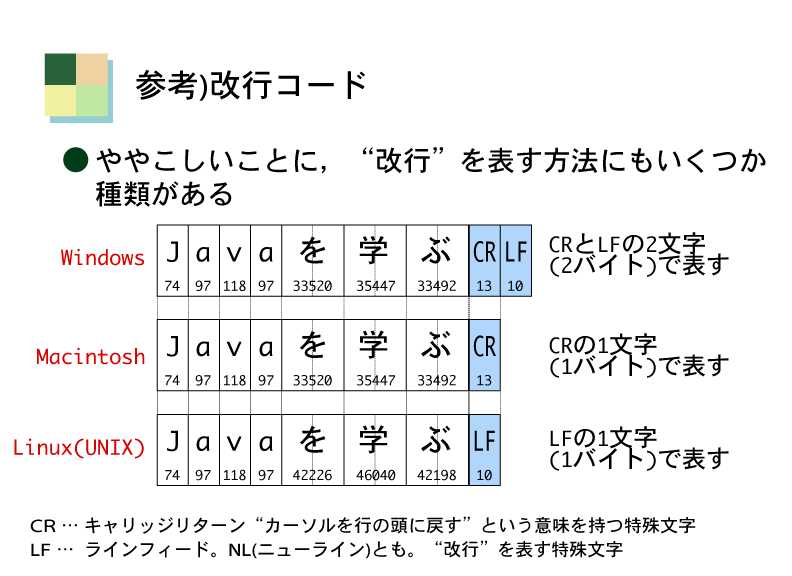
文字コードだけでなく,改行を表す目印も,オペレーティングシステムによって異なる(下図)。
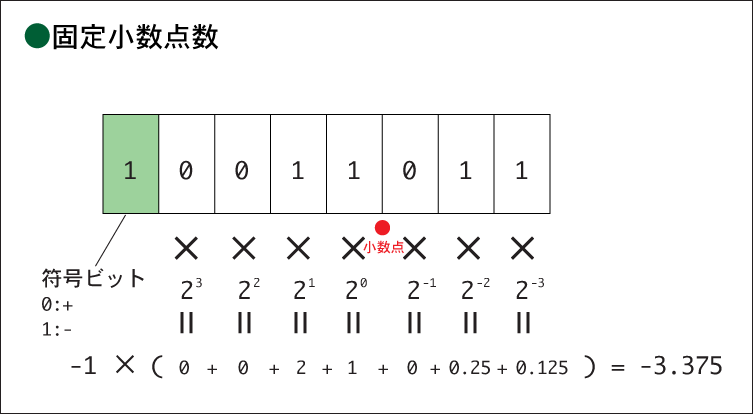
まず,固定小数点数を紹介する(下図)。この表現方法は,一番左のビットを正負を表すビットとして
使う(一番左のビットが0なら正数,1なら負数)。そして,小数点の場所を定めておく。下図の場合は,
右から3ビット目と4ビット目の間に小数点がある物として考える。
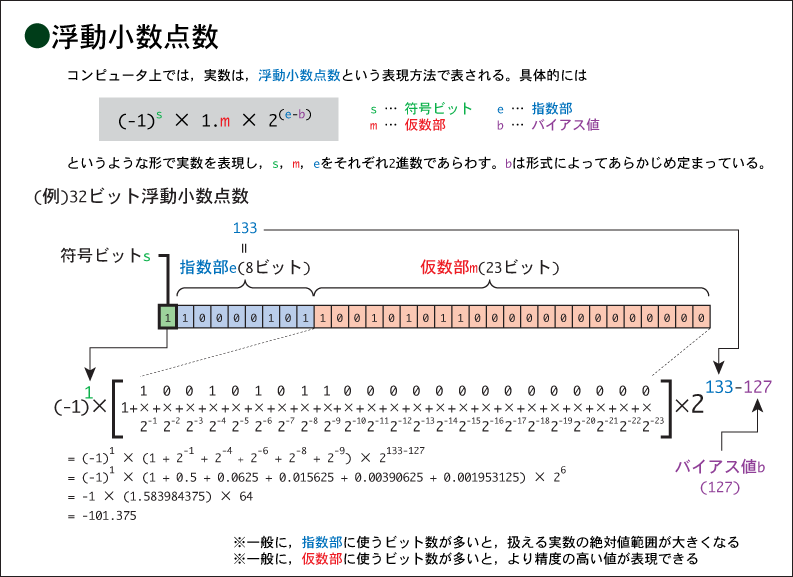
しかし,このように小数点の位置を固定するより,小数点の位置を随時ずらせるように
しておいた方が,柔軟に実数を表現できる。このように,小数点をずらせるようにした
実数の表現方法を,浮動小数点数(floating point number)と呼ぶ(下図)。下図は今はお
ぼえる必要はない。
以上のように,コンピュータ上では,ビットの集まりを使って,
・0以上の整数(符号なし整数)
・負数も含めた整数(符号付き整数)
・文字(0以上の整数で表現する)
・実数(浮動小数点数)
などが表現できるわけである。
C言語で使われるデータ型を紹介する。
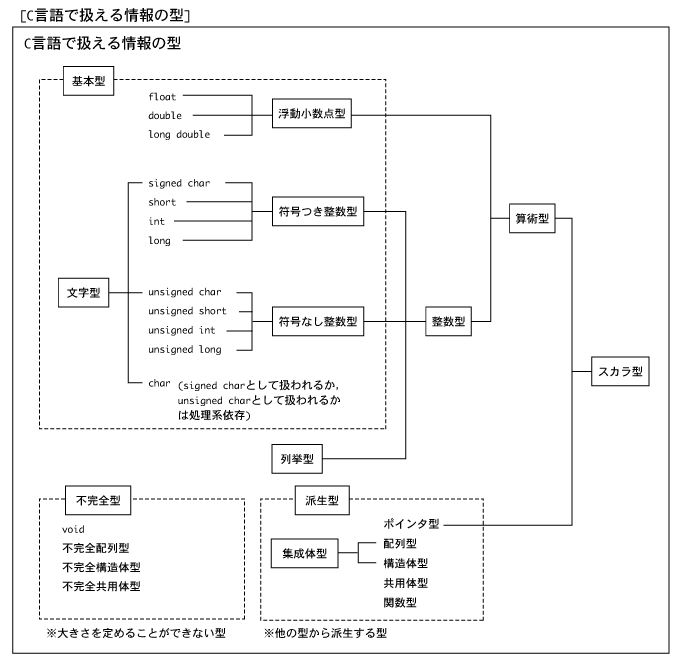
※「符合つき整数」は, signed int のように符合付き整数を表す signed をつけても良いが,上図のように省略できる。
ただし, char 型にかぎっては, signed または unsigned がついていない char型が「符合つき整数」になるか「符号なし整数」
になるかは,各コンパイラ製ごとに違っていて良い事になっている。
整数型は,下図(1)の様な範囲をカバーするようにC言語の規格で定められている。その上で,(2)のルールに従っていれば,
実際のデータ型のサイズは各コンパイラ製品ごとに異なっていて良い,とされている。

※自著「詳説C++ 第2版」より引用
※1バイトの符合付き整数は「2の補数記数法」では -128〜+127 まで表すことが出来るが,上図の様に signed char のカバーすべき範囲は -127〜+127 になっている。
これは, 符合付き整数を「2の補数記数法」ではなく,左端のビットを符号ビットとし,残りの7ビットを絶対値として表現する方法(-127〜+127を表せ,0は+0と-0の二つある)との
互換性を考慮しているためである。
※ひとつの計算式で,「符合つき整数」と「符号なし整数」を混ぜて計算してはいけない。