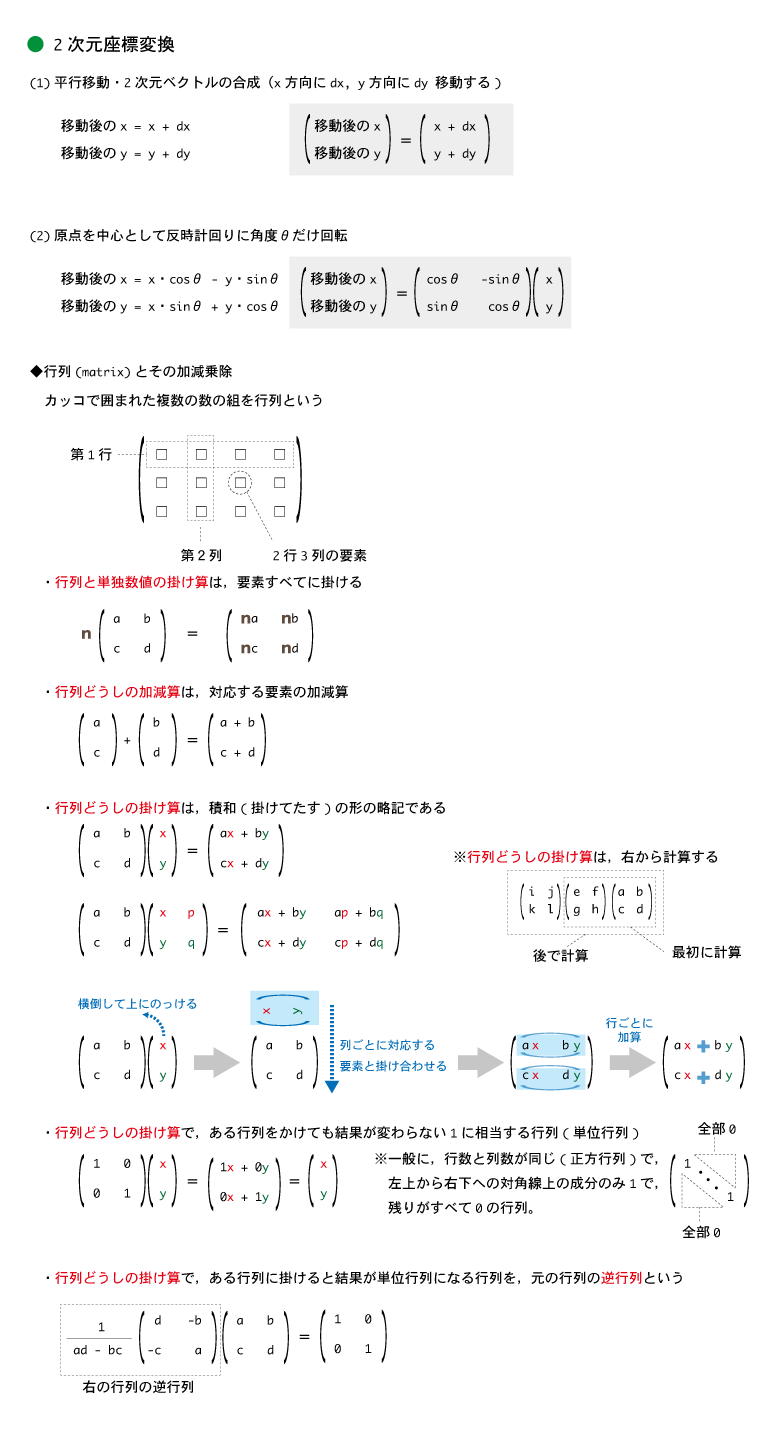
【座標計算の基礎】
【座標系】
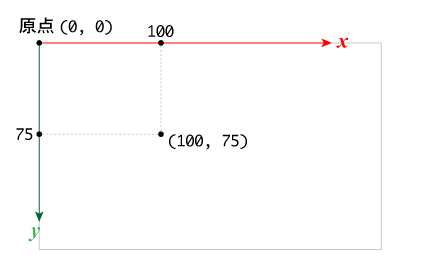
(1) 2次元座標系
コンピュータ画面上の2次元座標系は,「ゲームソフトウェア設計論」でも学習したように,一般にはy軸は下向きである。
描画対象領域の左上が原点となり,たいていは整数値で表され,単位としては pixel が使われる。

(2) 3次元座標系
・
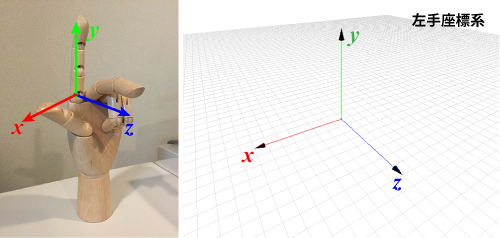
右手座標系と左手座標系
3次元座標系は,左手座標系または右手座標系で表される(下図)。ここでは,親指がX軸,人差し指がY軸,中指がZ軸である。
 |
 |
※ここでは,y軸を上方向としたが,zjik卯を上方向とする場合もある。
※座標値は実数値で表されるが,単位は決まっていないことが多く,決まっていてもソフトによってまちまちである(1.0が1.0mを表しているものもあれば,1.0cmを表してることもある)。
なお,XYZの座標軸は光の三原色のRGBになぞらえて,X軸が赤(R),Y軸が緑(G),Z軸が青(B)で表示されるのが一般的である。
| x | y | z |
| 親指 | 人差し指 | 中指 |
| 赤(R) | 緑(G) | 青(B) |
・ソフトによる座標系の違い
各ソフトウェアによっての採用している座標系は以下のとおり。
| ソフトウェア | DirectX/DXライブラリ | Unity | MMD | OpenGL | Metasequoia | Blender |
| 座標系 | 左手座標系 | 右手座標系 |
右手座標系 | |||
| 上向き | y軸 | z軸 | ||||
【ベクトルと座標変換】
ベクトル(vector,英語読みだとベクタ)とは,基本的には
・複数の数値を組にしたもの
(数ベクトル) 例:(1.0, 2.0, 3.0)
であるが,幾何学的には
・向きと大きさをもったもの (幾何ベクトル) (下図の矢印)
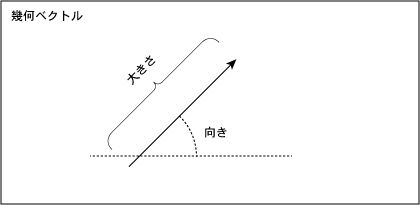
を言う。幾何ベクタは,「どこにあるか」は問題にならず,あくまで「向き」と「大きさ」だけをもったものである。
したがって,座標系で扱う時はその始点を原点に合わせて扱う(下図)。
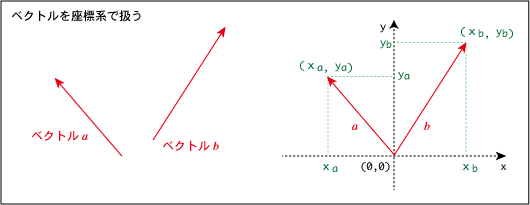
上図の様に,幾何ベクトルの始点を原点に揃えると,幾何ベクトルの終点の座標(これ自体は数ベクトル)で表現できる。
3次元でも同様である。
【DXライブラリでのベクトル表現】
・ DXライブラリでは,3次元座標値は単精度浮動小数点数型 ( float型 ) で表されている。
C/C++では, 1.2 というように小数点を含んだリテラル定数値を書くと double 型の値として扱われる。これをDXライブラリが float型値を要求するところに渡すと,
double→float の型変換作業が行われることになるので効率が悪い。 1.2f のように,末尾に f を付けると float型の実数値リテラルになるので, DXライブラリ用の
実数リテラルは,できるだけ末尾に f をつけておくこと。
・VECTOR構造体
DXライブラリでは,ヘッダファイル DxLib.h 内で 3次元ベクトルを表す VECTOR 構造体を次の様に定義している。
また,手軽に VECTOR構造体型の値を作成することができるVGet( ) 関数が用意されている(下図)。

・色の指定
DXライブラリでは, RGBそれぞれ 0〜255 で指定できる
色を利用できる。その際, GetColor( )関数でRGB値を指定し, unsigned int 型の色コードを返す関数
GetColor( ) が便利である。
・ベクトル演算関数
DXライブラリには,様々なベクトル演算関数が用意されている(「DXライブラリ 関数リファレンスページ 3D関係関数リファレンス」ページの「算術演算関数」の項を参照のことほうこう)。
#include <DxLib.h>
#include <cmath>
// 三次元の原点(VECTOR型はDXライブラリのヘッダで定義されている三次元座標を表す構造体)
VECTOR theOrigin = {0.0f, 0.0f, 0.0f};
/***
*** void draw3DArrow( float x0 = 0.0f, float y0 = 0.0f, float z0 = 0.0f,
*** float x1 = 1.0f, float y1 = 1.0f, float z1 = 1.0f, unsigned int theColor = VGet(255,0,0), float coneSize = 0.0f );
***
*** 三次元の矢印を始点( x0, y0, z0 ) 終点( x1, y1, z1 )間に描写する。色は色コードtheColor。
*** 矢印の先の円錐の高さを coneSize で指定する。coneSize の値が 0.0f の場合は、円錐の高さは自動調整される。
*** withArrow が true なら矢印の先の円錐を描画し、false なら描画しない。
***/
void draw3DArrow( float x0 = 0.0f, float y0 = 0.0f, float z0 = 0.0f,
float x1 = 1.0f, float y1 = 1.0f, float z1 = 1.0f, unsigned int theColor = GetColor(255,0,0), float coneSize = 0.0f, bool withArrow = true );
void draw3DArrow( float x0, float y0, float z0,
float x1, float y1, float z1, unsigned int theColor, float coneSize, bool withArrow ) {
VECTOR p0 = VGet( x0, y0, z0 );
VECTOR p1 = VGet( x1, y1, z1 );
DrawLine3D( p0, p1, theColor );
float len = sqrt( (x1-x0)* (x1-x0) + (y1-y0)*(y1-y0) + (z1-z0)*(z1-z0) );
if( withArrow ) {
if( coneSize <= 0.0f ) coneSize = len / 10.0f; // 矢印先の円錐の長さが0.0f以下に指定された場合は自動調整する。
float r = (len - coneSize) / len;
float xp = x0 + (x1-x0)*r;
float yp = y0 + (y1-y0)*r;
float zp = z0 + (z1-z0)*r;
DrawCone3D(VGet(x1, y1, z1), VGet( xp, yp, zp), coneSize / 4.0f, 12, theColor, theColor, TRUE);
}
}
/***
*** draw3DArrow( VECTOR p0 = VGet( 0.0f, 0.0f, 0.0f ), VECTOR p1 = VGet( 1.0f, 1.0f, 1.0f ),
*** unsigned int theColor = GetColor(255,0,0), float coneSize = 0.0f, bool withArrow = true );
***
*** 三次元の矢印を始点p0 終点p1間に描写する。色は色コードtheColor。矢印の先の円錐の高さを coneSize で指定する。
*** coneSize の値が 0.0f の場合は、円錐の高さは自動調整される。
*** withArrow が true なら矢印の先の円錐を描画し、false なら描画しない。
***/
void draw3DArrow( VECTOR p0 = VGet( 0.0f, 0.0f, 0.0f ), VECTOR p1 = VGet( 1.0f, 1.0f, 1.0f ), unsigned int theColor = GetColor(255,0,0), float coneSize = 0.0f, bool withArrow = true );
void draw3DArrow( VECTOR p0, VECTOR p1, unsigned int theColor, float coneSize, bool withArrow ) {
draw3DArrow(p0.x, p0.y, p0.z, p1.x, p1.y, p1.z, theColor, coneSize, withArrow );
}
/***
*** draw3DAxisArrow( float x0 = 0.0f, float y0 = 0.0f, float z0 = 0.0f, float length = 1.0f, bool withArrow = true );
*** (x0, y0, z0) を始点としたXYZ座標軸を描写する。X軸は赤、Y軸は緑、Z軸は青。
*** length は座標軸の長さ。withArrow が true の場合は、座標軸を円錐を使った矢印として描写する。
***/
void draw3DAxisArrow( float x0 = 0.0f, float y0 = 0.0f, float z0 = 0.0f, float length = 1.0f, bool withArrow = true );
void draw3DAxisArrow( float x0, float y0, float z0, float length, bool withArrow ) {
draw3DArrow( x0, y0, z0, x0 + length, y0, z0, GetColor(255, 0, 0), 0.0f, withArrow );
draw3DArrow( x0, y0, z0, x0, y0 + length, z0, GetColor(0, 255, 0), 0.0f, withArrow );
draw3DArrow( x0, y0, z0, x0, y0, z0 + length, GetColor(0, 0, 255), 0.0f, withArrow );
}
/***
*** void drawXZPlane( int numOfMesh, float meshInterval, bool FillFlag = true );
*** numOfMesh 個の格子(一辺の長さは meshInterval )で、原点を中心としたXZ平面を描写する。
*** FillFlag が true の場合は、平面を白く塗りつぶし、false の場合は塗りつぶさない。
***/
void drawXZPlane( int numOfMesh, float meshInterval, bool FillFlag = true );
void drawXZPlane( int numOfMesh, float meshInterval, bool FillFlag ) {
float width = numOfMesh * meshInterval;
float x0 = - width / 2.0f;
float z0 = x0;
unsigned int lineColor = GetColor(220, 220, 220);
// FillFlag が true なら、平面(原点を中心とした一辺が width の正方形領域)を白で塗りつぶす(実際には白い三角ポリゴンを2個描写する)。
if( FillFlag ) {
DrawTriangle3D( VGet( x0, 0.0f, z0), VGet(x0, -0.0f, -z0), VGet(-x0, 0.0f, z0), GetColor(255,255,255), true );
DrawTriangle3D( VGet(-x0, 0.0f, -z0), VGet(x0, -0.0f, -z0), VGet(-x0, 0.0f, z0), GetColor(255,255,255), true );
lineColor = GetColor(220, 220, 220);
}
// 格子線を描写する。
for(int n = 0; n <= numOfMesh; n++ ) {// Z軸に平行な平行線分を書く。
float ratio = n / (1.0f * numOfMesh);
float offset = ratio * width;
DrawLine3D( VGet(x0 + offset, 0.0f, z0), VGet(x0 + offset, 0.0f, -z0), lineColor );
}
for(int n = 0; n <= numOfMesh; n++ ) {// X軸に平行な平行線分を書く。
float ratio = n / (1.0f * numOfMesh);
float offset = ratio * width;
DrawLine3D( VGet(x0, 0.0f, z0 + offset), VGet(-x0, 0.0f, z0 + offset), lineColor );
}
}
/***
*** void drawRectangle( VECTOR p0, VECTOR p1, VECTOR p2, VECTOR p3, unsigned int color = GetColor(255,255,255) );
*** 4頂点を p0, p1, p2, p3 とする color 色の矩形を描写する。なお、頂点 p0とp2 は対角頂点である事。
***
***/
void drawRectangle( VECTOR p0, VECTOR p1, VECTOR p2, VECTOR p3, unsigned int color = GetColor(255,255,255) );
void drawRectangle( VECTOR p0, VECTOR p1, VECTOR p2, VECTOR p3, unsigned int color ) {
DrawTriangle3D( p0, p1, p2, color, true );
DrawTriangle3D( p2, p3, p0, color, true );
}
/***
*** void drawCube( VECTOR center, float width, unsigned int color = GetColor(255,255,255) );
*** 中心点 center を囲む一辺の長さが width の立方体を描写する。面の色は color で指定する。
*** 尚、各面はXY平面、YZ平面、XZ平面のいずれかに平行である。
***
***/
void drawCube( VECTOR center, float width, unsigned int color = GetColor(255,255,255) );
void drawCube( VECTOR center, float width, unsigned int color ) {
float x = center.x;
float y = center.y;
float z = center.z;
float s = width / 2.0f;
// 立方体の8頂点を取得する。
VECTOR v_XYZ = VGet( x + s, y + s, z + s );
VECTOR v_XYz = VGet( x + s, y + s, z - s );
VECTOR v_XyZ = VGet( x + s, y - s, z + s );
VECTOR v_xYZ = VGet( x - s, y + s, z + s );
VECTOR v_Xyz = VGet( x + s, y - s, z - s );
VECTOR v_xYz = VGet( x - s, y + s, z - s );
VECTOR v_xyZ = VGet( x - s, y - s, z + s );
VECTOR v_xyz = VGet( x - s, y - s, z - s );
// 立方体の面を描画する。
drawRectangle( v_XYZ, v_XYz, v_Xyz, v_XyZ, color );
drawRectangle( v_XYZ, v_xYZ, v_xYz, v_XYz, color );
drawRectangle( v_xyz, v_Xyz, v_XYz, v_xYz, color );
drawRectangle( v_Xyz, v_XyZ, v_xyZ, v_xyz, color );
drawRectangle( v_XYZ, v_xYZ, v_xyZ, v_XyZ, color );
drawRectangle( v_xyz, v_xyZ ,v_xYZ, v_xYz, color );
}
int WINAPI WinMain( HINSTANCE, HINSTANCE, LPSTR, int ){
ChangeWindowMode( TRUE ); // ゲーム画面をウィンドウで表示するように指定する。
DxLib_Init(); // DXライブラリを初期化する。
SetDrawScreen( DX_SCREEN_BACK ); // 描写先を裏画面にする。
//カメラの描写範囲(奥行)を0.1〜10000.0に設定する。
SetCameraNearFar( 0.1f, 10000.0f );
//( 0.0, 9.0, -22.0 )の位置にカメラを設置し、視線を( 0.0, 10.0, 0.0 )にあるターゲットへ向ける。
VECTOR cameraPos = VGet( 0.0f, 9.0f, -22.0f );
VECTOR theTarget = VGet( 0.0f, 10.0f, 0.0f );
bool targeIsOrigin = false;
SetCameraPositionAndTarget_UpVecY( cameraPos, theTarget );
//Zバッファを使って図形描写を行う。
SetUseZBuffer3D( TRUE );
SetWriteZBuffer3D( TRUE );
// 繰り返し。
while( ! ProcessMessage() ){
// 描写先の画面(裏画面)を消去する。
ClearDrawScreen();
// 原点を囲むように、一辺が 100.f の白い立方体を描写する。
drawCube( VGet(0.0f, 0.0f, 0.0f), 200.0f );
// XZ平面を描写する。
drawXZPlane( 100, 1.0, false );
// 座標軸を描写する。
draw3DAxisArrow( 0.0f, 0.0f, 0.0f, 8.0f );
// カメラの座標を画面左下に表示する。
DrawFormatString( 0, 460, GetColor(0,0,0), "%6.2f, %6.2f, %6.2f", cameraPos.x, cameraPos.y, cameraPos.z );
// 完成した裏画面の内容を表画面(ゲームのウィンドウ)に転写する。
ScreenFlip();
// キー(ゲームコントローラー)の状態を得る。
int keyInput = GetJoypadInputState( DX_INPUT_KEY_PAD1 );
// カメラ(とターゲット)の位置を変更する
if( keyInput == PAD_INPUT_DOWN ) {
cameraPos.z = cameraPos.z - 0.5; theTarget.z = theTarget.z - 0.5f;
}
if( keyInput == PAD_INPUT_UP ) {
cameraPos.z = cameraPos.z + 0.5; theTarget.z = theTarget.z + 0.5f;
}
if( keyInput == PAD_INPUT_LEFT ) {
cameraPos.x = cameraPos.x - 0.5; theTarget.x = theTarget.x - 0.5f;
}
if( keyInput == PAD_INPUT_RIGHT ) {
cameraPos.x = cameraPos.x + 0.5; theTarget.x = theTarget.x + 0.5f;
}
char c = GetInputChar( TRUE );
if( c == 'u' ) {
cameraPos.y = cameraPos.y + 0.5f; theTarget.y = theTarget.y + 0.5f;
}
if( c == 'n' ) {
cameraPos.y = cameraPos.y - 0.5f; theTarget.y = theTarget.y - 0.5f;
}
if( c == 't' ) { // カメラのターゲットを標準位置にするか原点にするか切り替える。
targeIsOrigin = !targeIsOrigin;
}
// カメラの位置を設定しなおす。
if( targeIsOrigin ) { // targeIsOrigin が true なら、カメラをターゲットに向ける。
SetCameraPositionAndTarget_UpVecY( cameraPos, VGet(0.0f, 0.0f, 0.0f) );
}
else { // targeIsOrigin が false なら、カメラを標準位置に向ける。
SetCameraPositionAndTarget_UpVecY( cameraPos, theTarget );
}
}
DxLib_End(); // DXライブラリの後処理を行う.
return 0 ;
}
#include <DxLib.h>
#include <cmath>
// 三次元の原点(VECTOR型はDXライブラリのヘッダで定義されている三次元座標を表す構造体)
VECTOR theOrigin = { 0.0f, 0.0f, 0.0f };
/***
*** void draw3DArrow( float x0 = 0.0f, float y0 = 0.0f, float z0 = 0.0f,
*** float x1 = 1.0f, float y1 = 1.0f, float z1 = 1.0f, unsigned int theColor = VGet(255,0,0), float coneSize = 0.0f );
***
*** 三次元の矢印を始点( x0, y0, z0 ) 終点( x1, y1, z1 )間に描写する。色は色コードtheColor。
*** 矢印の先の円錐の高さを coneSize で指定する。coneSize の値が 0.0f の場合は、円錐の高さは自動調整される。
*** withArrow が true なら矢印の先の円錐を描画し、false なら描画しない。
***/
void draw3DArrow(float x0 = 0.0f, float y0 = 0.0f, float z0 = 0.0f,
float x1 = 1.0f, float y1 = 1.0f, float z1 = 1.0f, unsigned int theColor = GetColor(255, 0, 0), float coneSize = 0.0f, bool withArrow = true);
void draw3DArrow(float x0, float y0, float z0,
float x1, float y1, float z1, unsigned int theColor, float coneSize, bool withArrow) {
VECTOR p0 = VGet(x0, y0, z0);
VECTOR p1 = VGet(x1, y1, z1);
DrawLine3D(p0, p1, theColor);
float len = sqrt((x1 - x0)* (x1 - x0) + (y1 - y0)*(y1 - y0) + (z1 - z0)*(z1 - z0));
if (withArrow) {
if (coneSize <= 0.0f) coneSize = len / 10.0f; // 矢印先の円錐の長さが0.0f以下に指定された場合は自動調整する。
float r = (len - coneSize) / len;
float xp = x0 + (x1 - x0)*r;
float yp = y0 + (y1 - y0)*r;
float zp = z0 + (z1 - z0)*r;
DrawCone3D(VGet(x1, y1, z1), VGet(xp, yp, zp), coneSize / 4.0f, 12, theColor, theColor, TRUE);
}
}
/***
*** draw3DArrow( VECTOR p0 = VGet( 0.0f, 0.0f, 0.0f ), VECTOR p1 = VGet( 1.0f, 1.0f, 1.0f ),
*** unsigned int theColor = GetColor(255,0,0), float coneSize = 0.0f, bool withArrow = true );
***
*** 三次元の矢印を始点p0 終点p1間に描写する。色は色コードtheColor。矢印の先の円錐の高さを coneSize で指定する。
*** coneSize の値が 0.0f の場合は、円錐の高さは自動調整される。
*** withArrow が true なら矢印の先の円錐を描画し、false なら描画しない。
***/
void draw3DArrow(VECTOR p0 = VGet(0.0f, 0.0f, 0.0f), VECTOR p1 = VGet(1.0f, 1.0f, 1.0f), unsigned int theColor = GetColor(255, 0, 0), float coneSize = 0.0f, bool withArrow = true);
void draw3DArrow(VECTOR p0, VECTOR p1, unsigned int theColor, float coneSize, bool withArrow) {
draw3DArrow(p0.x, p0.y, p0.z, p1.x, p1.y, p1.z, theColor, coneSize, withArrow);
}
/***
*** draw3DAxisArrow( float x0 = 0.0f, float y0 = 0.0f, float z0 = 0.0f, float length = 1.0f, bool withArrow = true );
*** (x0, y0, z0) を始点としたXYZ座標軸を描写する。X軸は赤、Y軸は緑、Z軸は青。
*** length は座標軸の長さ。withArrow が true の場合は、座標軸を円錐を使った矢印として描写する。
***/
void draw3DAxisArrow(float x0 = 0.0f, float y0 = 0.0f, float z0 = 0.0f, float length = 1.0f, bool withArrow = true);
void draw3DAxisArrow(float x0, float y0, float z0, float length, bool withArrow) {
draw3DArrow(x0, y0, z0, x0 + length, y0, z0, GetColor(255, 0, 0), 0.0f, withArrow);
draw3DArrow(x0, y0, z0, x0, y0 + length, z0, GetColor(0, 255, 0), 0.0f, withArrow);
draw3DArrow(x0, y0, z0, x0, y0, z0 + length, GetColor(0, 0, 255), 0.0f, withArrow);
}
/***
*** void drawXZPlane( int numOfMesh, float meshInterval, bool FillFlag = true );
*** numOfMesh 個の格子(一辺の長さは meshInterval )で、原点を中心としたXZ平面を描写する。
*** FillFlag が true の場合は、平面を白く塗りつぶし、false の場合は塗りつぶさない。
***/
void drawXZPlane(int numOfMesh, float meshInterval, bool FillFlag = true);
void drawXZPlane(int numOfMesh, float meshInterval, bool FillFlag) {
float width = numOfMesh * meshInterval;
float x0 = -width / 2.0f;
float z0 = x0;
unsigned int lineColor = GetColor(220, 220, 220);
// FillFlag が true なら、平面(原点を中心とした一辺が width の正方形領域)を白で塗りつぶす(実際には白い三角ポリゴンを2個描写する)。
if (FillFlag) {
DrawTriangle3D(VGet(x0, 0.0f, z0), VGet(x0, -0.0f, -z0), VGet(-x0, 0.0f, z0), GetColor(255, 255, 255), true);
DrawTriangle3D(VGet(-x0, 0.0f, -z0), VGet(x0, -0.0f, -z0), VGet(-x0, 0.0f, z0), GetColor(255, 255, 255), true);
lineColor = GetColor(220, 220, 220);
}
// 格子線を描写する。
for (int n = 0; n <= numOfMesh; n++) {// Z軸に平行な平行線分を書く。
float ratio = n / (1.0f * numOfMesh);
float offset = ratio * width;
DrawLine3D(VGet(x0 + offset, 0.0f, z0), VGet(x0 + offset, 0.0f, -z0), lineColor);
}
for (int n = 0; n <= numOfMesh; n++) {// X軸に平行な平行線分を書く。
float ratio = n / (1.0f * numOfMesh);
float offset = ratio * width;
DrawLine3D(VGet(x0, 0.0f, z0 + offset), VGet(-x0, 0.0f, z0 + offset), lineColor);
}
}
/***
*** void drawRectangle( VECTOR p0, VECTOR p1, VECTOR p2, VECTOR p3, unsigned int color = GetColor(255,255,255) );
*** 4頂点を p0, p1, p2, p3 とする color 色の矩形を描写する。なお、頂点 p0とp2 は対角頂点である事。
***
***/
void drawRectangle(VECTOR p0, VECTOR p1, VECTOR p2, VECTOR p3, unsigned int color = GetColor(255, 255, 255));
void drawRectangle(VECTOR p0, VECTOR p1, VECTOR p2, VECTOR p3, unsigned int color) {
DrawTriangle3D(p0, p1, p2, color, true);
DrawTriangle3D(p2, p3, p0, color, true);
}
/***
*** void drawCube( VECTOR center, float width, unsigned int color = GetColor(255,255,255) );
*** 中心点 center を囲む一辺の長さが width の立方体を描写する。面の色は color で指定する。
*** 尚、各面はXY平面、YZ平面、XZ平面のいずれかに平行である。
***
***/
void drawCube(VECTOR center, float width, unsigned int color = GetColor(255, 255, 255));
void drawCube(VECTOR center, float width, unsigned int color) {
float x = center.x;
float y = center.y;
float z = center.z;
float s = width / 2.0f;
// 立方体の8頂点を取得する。
VECTOR v_XYZ = VGet(x + s, y + s, z + s);
VECTOR v_XYz = VGet(x + s, y + s, z - s);
VECTOR v_XyZ = VGet(x + s, y - s, z + s);
VECTOR v_xYZ = VGet(x - s, y + s, z + s);
VECTOR v_Xyz = VGet(x + s, y - s, z - s);
VECTOR v_xYz = VGet(x - s, y + s, z - s);
VECTOR v_xyZ = VGet(x - s, y - s, z + s);
VECTOR v_xyz = VGet(x - s, y - s, z - s);
// 立方体の面を描画する。
drawRectangle(v_XYZ, v_XYz, v_Xyz, v_XyZ, color);
drawRectangle(v_XYZ, v_xYZ, v_xYz, v_XYz, color);
drawRectangle(v_xyz, v_Xyz, v_XYz, v_xYz, color);
drawRectangle(v_Xyz, v_XyZ, v_xyZ, v_xyz, color);
drawRectangle(v_XYZ, v_xYZ, v_xyZ, v_XyZ, color);
drawRectangle(v_xyz, v_xyZ, v_xYZ, v_xYz, color);
}
int WINAPI WinMain(HINSTANCE, HINSTANCE, LPSTR, int){
ChangeWindowMode(TRUE); // ゲーム画面をウィンドウで表示するように指定する。
DxLib_Init(); // DXライブラリを初期化する。
SetDrawScreen(DX_SCREEN_BACK); // 描写先を裏画面にする。
// MMDキャラクタモデルと背景モデルをモーション付きで描画するために必要な変数群
int modelHandle1, modelHandle_BG; // 読み込んだ3Dモデルデータの番号を記録しておく変数
int attachIndex; // アタッチされたアニメーションの番号を記録しておく変数
float animTime000; // アニメーションの総再生時間を記録しておく変数
float theTime; // アニメーションの再生時間を記録しておく変数
// 以下,(1)〜(8)は, MMDキャラクタモデルと背景モデルを描写するための処理
// (1)3Dモデルデータの読み込み
modelHandle1 = MV1LoadModel("那珂ver1.01/那珂ver1.0.1.pmd");
modelHandle_BG = MV1LoadModel("かぼちゃステージ/カボチャステージ(空セット).pmx");
// (2) 3Dモデル1に対してアニメーション0番をアタッチする
attachIndex = MV1AttachAnim(modelHandle1, 0, -1, FALSE);
// (3) アタッチしたアニメーションの再生時間を得る
animTime000 = MV1GetAttachAnimTotalTime(modelHandle1, attachIndex);
// (4) ゲーム内時間の初期化
theTime = 0.0;
//カメラの描写範囲(奥行)を0.1〜10000.0に設定する。
SetCameraNearFar(0.1f, 10000.0f);
//( 0.0, 9.0, -22.0 )の位置にカメラを設置し、視線を( 0.0, 10.0, 0.0 )にあるターゲットへ向ける。
VECTOR cameraPos = VGet(0.0f, 9.0f, -22.0f);
VECTOR theTarget = VGet(0.0f, 10.0f, 0.0f);
bool targeIsOrigin = false;
SetCameraPositionAndTarget_UpVecY(cameraPos, theTarget);
//Zバッファを使って図形描写を行う。
SetUseZBuffer3D(TRUE);
SetWriteZBuffer3D(TRUE);
// 繰り返し。
while (!ProcessMessage()){
// 描写先の画面(裏画面)を消去する。
ClearDrawScreen();
// 原点を囲むように、一辺が 100.f の白い立方体を描写する。
drawCube(VGet(0.0f, 0.0f, 0.0f), 200.0f);
// (5) 現在の再生時間をセットする
MV1SetAttachAnimTime(modelHandle1, attachIndex, theTime);
// (6) 3Dモデルの描画
MV1DrawModel(modelHandle_BG);
MV1DrawModel(modelHandle1);
// XZ平面を描写する。
drawXZPlane(100, 1.0, false);
// 座標軸を描写する。
draw3DAxisArrow(0.0f, 0.0f, 0.0f, 20.0f);
// カメラの座標を画面左下に表示する。
DrawFormatString(0, 460, GetColor(0, 0, 0), "%6.2f, %6.2f, %6.2f", cameraPos.x, cameraPos.y, cameraPos.z);
// 完成した裏画面の内容を表画面(ゲームのウィンドウ)に転写する。
ScreenFlip();
// キー(ゲームコントローラー)の状態を得る。
int keyInput = GetJoypadInputState(DX_INPUT_KEY_PAD1);
// カメラ(とターゲット)の位置を変更する
if (keyInput == PAD_INPUT_DOWN) {
cameraPos.z = cameraPos.z - 0.5; theTarget.z = theTarget.z - 0.5f;
}
if (keyInput == PAD_INPUT_UP) {
cameraPos.z = cameraPos.z + 0.5; theTarget.z = theTarget.z + 0.5f;
}
if (keyInput == PAD_INPUT_LEFT) {
cameraPos.x = cameraPos.x - 0.5; theTarget.x = theTarget.x - 0.5f;
}
if (keyInput == PAD_INPUT_RIGHT) {
cameraPos.x = cameraPos.x + 0.5; theTarget.x = theTarget.x + 0.5f;
}
char c = GetInputChar(TRUE);
if (c == 'u') {
cameraPos.y = cameraPos.y + 0.5f; theTarget.y = theTarget.y + 0.5f;
}
if (c == 'n') {
cameraPos.y = cameraPos.y - 0.5f; theTarget.y = theTarget.y - 0.5f;
}
if (c == 't') { // カメラのターゲットを標準位置にするか原点にするか切り替える。
targeIsOrigin = !targeIsOrigin;
}
// カメラの位置を設定しなおす。
if (targeIsOrigin) { // targeIsOrigin が true なら、カメラをターゲットに向ける。
SetCameraPositionAndTarget_UpVecY(cameraPos, VGet(0.0f, 0.0f, 0.0f));
}
else { // targeIsOrigin が false なら、カメラを標準位置に向ける。
SetCameraPositionAndTarget_UpVecY(cameraPos, theTarget);
}
// (7) 次の描写のためにゲーム内時間を更新する
theTime = theTime + 0.4;
// (8) ゲーム内時間がアニメーションの再生時間を超えたら再生時間をリセットする
if (theTime >= animTime000) theTime = 0.0;
}
DxLib_End(); // DXライブラリの後処理を行う.
return 0;
}
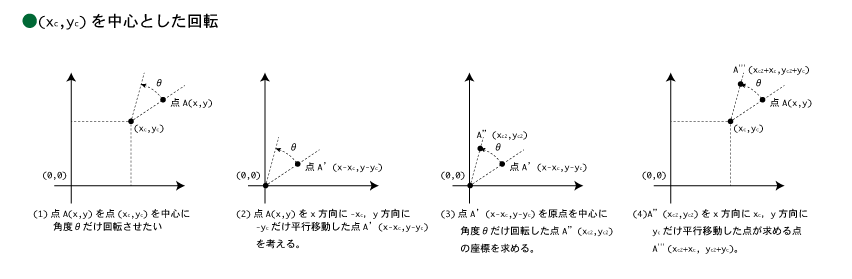
●座標変換を組み合わせた例
●提出課題 第14回(2025/01/09)出題課題 2026/01/23(金) 09:15 締切
List 2に処理を追加し,点A(2.0, 0.5, 0.0)を中心としてXY平面と平行な面の上で半径0.2の球を反時計回りに回転させるように表示せよ。
なお,Aからこの球の中心までの距離は2.0とする。
球を描写するには,DXライブラリリファレンスページの3D関係関数のDrawSphere3D関数を使えば良い。
こちらのリンク先から提出せよ(先のリンク先に動作例の動画も掲載しているので参照せよ)。締切は 2026/01/23(金) 09:15。
ヒント:
(0)まず,このサンプル1で,処理を書く場所を確認する(3箇所。1箇所目は必要な変数の宣言。2箇所目は球の描写。3箇所目は座標の変換)。
(1)次に,原点を中心に半径0.2の球を描写してみよう(サンプル2)。
(2)次に,以下の様な処理を書き直す。サンプル3は,処理1のX座標に関する処理と処理3のX座標に関する処理だけ記入済み。
処理1:回転の中心点を原点へ平行移動する(球の中心も同じ量だけ平行移動する)
処理2:原点を中心としてxy平面上で theta ラジアンだけ回転
処理3:回転の中心点を元の位置へ平行移動する(球の中心も同じ量だけ平行移動する)
