| 総合情報論 (環境情報学科1年次後期配当 金曜日3限) 大城クラス |
●探索(search)とは,データ構造の中から目的のデータを探し出す操作のことである
探索にも,様々なアルゴリズムがある
●線形探索法
線形探索法(sequential search)は,データ列の最初の要素から順々に要素を調べていき,目的のデータ
を探すと言うアルゴリズムである。N個要素が有れば,平均してN/2回で目的の要素を見つけることが出来
る。以下に,実際のプログラム例を示す。
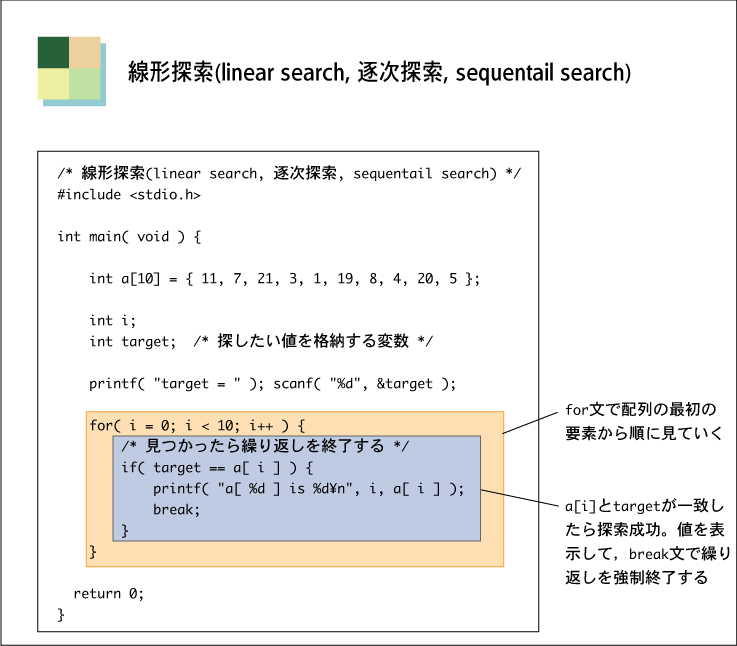
linearsearch.c
●2分探索法
2分探索法(binary search)は,あらかじめ整列されたデータ列を用いる。そして,範囲を2分して,目的
のデータがどちらの範囲にあるか判断し,さらにその範囲を2分する。これを繰り返すことで,範囲をしぼ
っていき,目的のデータを探す。
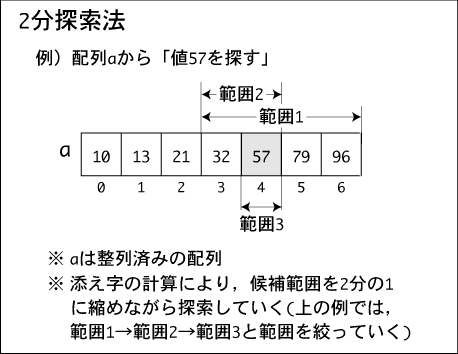
実際にプログラムにする場合,要素列が昇順で並んでいる例では,
(1)まず要素列の中央要素を調べ,その値が探索値に等しければ探索成功
(2)そうでなければ,
(a)探索値<中央要素の値 なら,探索範囲を中央要素の左の区間にする
(b)中央要素の値<探索値 なら,探索範囲を中央要素の右の区間にする
というように書く。以下に,実際のプログラム例を示す。

binarysearch.c
2分探索は効率が良く,N個の要素がある場合,そのオーダは O(log N) であり,これは O(N)より小さい。
つまり,線形探索より効率が良い。しかし,あらかじめデータを整列しておかなければならない。また,
ランダムアクセスの高速性に頼っているので,配列を使用せざるをえない。これらの理由から,データを
頻繁に挿入・削除するようなケースにはあまり向いていない。
●平衡探索木を使った探索法
平衡探索木(balanced search tree)と呼ばれる特殊な木構造を使う探索法がある。
平衡探索木とは,
・各頂点に対して,左の子≦親,親≦右の子,という条件が成立していて,
・左右にバランスがとれた
2分木のことである。
このような木で,根から探索を始め,探索値と頂点の値が同じなら探索成功とし,
(1)探索値が頂点の値と同じなら,探索成功
(2)そうでないなら
(a)探索値が頂点の値より小さい場合は,左の子へ探索していく
(b)探索値が頂点の値より大きい場合は,右の子へ探索していく
という探索法である。
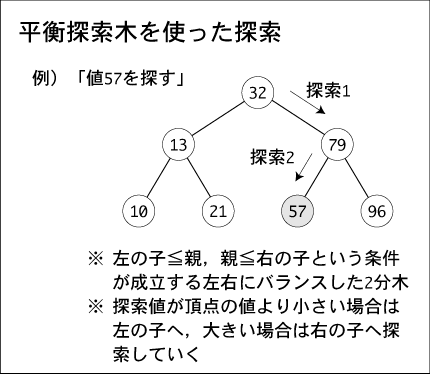
平衡探索木を使った探索法も,2分探索法の一種で,やはり O(log N)のオーダで探索できる高速な探索法
である。しかし,前述したように木構造はリストのように,ポインタで要素を繋いでいるため,要素の挿入や削除が高速に行える。この点から,探索には平衡探索木が使われることが多い。



